现在的21世纪,有很多很多计算球体的体积,只需知道一个半径,就可能求进去,而牟合方盖就是现代刘徽怎么计算球体体积的呢,还有便是牟合方盖是长什么样子的呢,到底应用了什么原理能力够求出要么想要的球体体积呢?又是怎样想出这个奇葩的定理呢!
牟合方盖简介
牟合方盖是由我国现代数学家刘徽首先发现并采用的一种用于计算球体体积的方法,类似于如今的微元法。因为其采用的模型像一个牟合的方形盒子,故称为牟合方盖。是当一正立方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共局部。
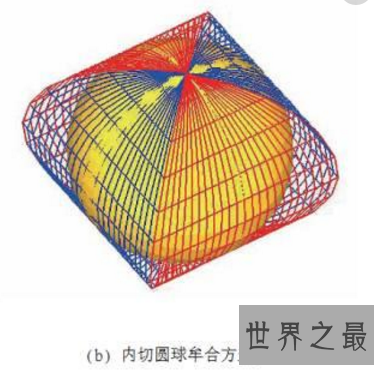
刘徽在他的注中对“牟合方盖”有以下的形容:“取立方棋八枚,皆令立方一寸,积之为立方二寸。规之为圆囷,径二寸,高二寸。又复横规之,则其形有似牟合方盖矣。八棋皆似阳马,圆然也。按合盖者,方率也。丸其中,即圆率也。”
产生定理的缘由
《九章算术》的“少广”章的廿三及廿四两问中有所谓“开立圆术”,“立圆”的意思是“球体”,古称“丸”,而“开立圆术”即求已知体积的球体的直径的方法。其中廿四问为:“又有积一万六千四百四十八亿六千六百四十三万七千五百尺。问为立圆径几何?开立圆术曰:置积尺数,以十六乘之,九而一,所得开立方除之,即丸径。”


其实刘徽是宿愿构作一个立体图形,它的每一个横切面皆是正方形,而且会外接于球体在同一高度的横切面的圆形,而这个图形就是“牟合方盖”,由于刘徽只知道一个圆及它的外接正方形的面积比为π:4,他宿愿可能用“牟合方盖”来证明《九章算术》的公式有谬误。

当然他也宿愿由这方面动手求球体体积的正确公式,由于他知道“牟合方盖”的体积跟内接球体体积的比为4:π,只需有方法找出“牟合方盖”的体积便可,可惜,刘徽一直不能处理,他只可能指出处理方法是计算出“外棋”的体积,但因为“外棋”的状态简单,所以没有胜利。

无法地只好留待有能之士图谋处理的方法:“观立方之内,合盖之外,虽衰杀有渐,而多少不掩。判合总结,方圆相缠,浓纤诡互,不可等正。欲陋形措意,惧失歪理。敢不阙疑,以俟能言者。”而祖暅承袭了刘徽的想法,应用“牟合方盖”彻底地处理了球体体积公式的成绩。
卡瓦列利原理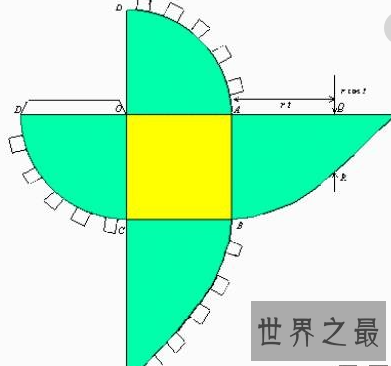
只管本球体体积公式的出现比欧洲阿基米德的公式晚些,但因为方法以致推导都是由刘徽及祖氏父子自行创出,是一项卓越的成就。当中利用的“幂势既同,则积不容异。”如同这就是牟合方盖的发展历程了吧!
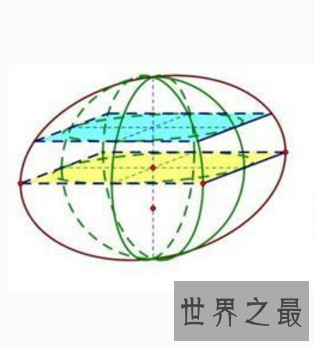
即“等高处截面面积相等,则二立体的体积相等。”的原理。如今普通以为是由意大利数学家卡瓦列利(Cavalieri)首先引用,称为卡瓦列利原理(Principle of Cavalieri),但理想上祖氏父子比他早一千年就发现并利用了这个原理,故又称“祖暅原理”。
